À titre de remarque liminaire, il convient d’observer que, conformément à l’article R. 314-1 du Code de la consommation, le calcul du TEG/TAEG repose sur l’hypothèse que le contrat de crédit restera valable pendant la durée convenue et que le prêteur et l’emprunteur rempliront leurs obligations selon les conditions et dans les délais précisés dans le contrat de crédit.

Cette disposition précise que, s’agissant des contrats de crédit qui comportent des clauses qui permettent des adaptations du taux d’intérêt et, le cas échéant, des frais entrant dans le taux effectif global mais ne pouvant pas faire l’objet d’une quantification au moment du calcul, le TEG/TAEG est calculé en partant de l’hypothèse que le taux d’intérêt et les autres frais resteront fixes par rapport au niveau initial et s’appliqueront jusqu’au terme du contrat de crédit.

L’article L. 312-2 du Code de la consommation ajoute que lorsque le prêt fait l’objet d’un amortissement échelonné, le taux effectivement pratiqué doit, en toute hypothèse, être calculé en tenant compte des modalités de l’amortissement de la créance.

Pour le reste, il convient de distinguer selon que le coût du crédit s’exprime en TEG ou en TAEG.

I) Le calcul du TEG : la méthode proportionnelle

L’article R. 314-2 du Code de la consommation dispose que « pour les opérations de crédit destinées à financer les besoins d’une activité professionnelle ou destinées à des personnes morales de droit public, le taux effectif global est un taux annuel, proportionnel au taux de période, à terme échu et exprimé pour cent unités monétaires. »

Deux enseignements peuvent être tirés de cette disposition.

D’une part, pour les crédits consentis à des professionnels où à des personnes morales de droit public, le coût du crédit s’exprime en taux effectif global.

D’autre part, le taux effectif global, applicable à cette catégorie de crédit, se calcule selon la méthode que l’on qualifie de proportionnelle.

La spécificité de cette méthode de calcul du taux d’intérêt est qu’elle s’effectue en deux temps.

Dans un premier temps, il convient de calculer ce que l’on appelle un taux de période, lequel correspond à la périodicité des remboursements effectués par l’emprunteur (mois, trimestre, semestre, etc…).

À cet égard, l’alinéa 2 de l’article R. 314-2 du Code de la consommation précise que « lorsque la périodicité des versements est irrégulière, la période unitaire est celle qui correspond au plus petit intervalle séparant deux versements. Le plus petit intervalle de calcul ne peut cependant être inférieur à un mois. ».

En tout état de cause, le taux de période est calculé actuariellement, à partir d’une période unitaire correspondant à la périodicité des versements effectués par l’emprunteur.

Cette opération mathématique consiste à ramener des flux financiers non directement comparables, car se produisant à des dates différentes, à une même base, en calculant la valeur actualisée de chaque flux futur, positif ou négatif, de remboursement, de paiement d’intérêt ou autre, ce qui donne la valeur actualisée.

Pour bien comprendre la logique qui préside à cette méthode de calcul, il convient de partir du constat que les modalités de paiement des intérêts diffèrent d’un emprunt à l’autre. Or payer les intérêts dus chaque année pour un emprunt en une seule fois à la fin de la période annuelle, ne revient pas au même que de payer les intérêts chaque mois.

Supposons, par exemple, que l’on emprunte la somme de 10.000 euros laquelle doit être entièrement remboursée au bout d’un an, avec un taux d’intérêt nominal de 12%.

Dans l’hypothèse où les intérêts sont payés chaque mois, l’emprunteur doit régler au prêteur chaque mois un douzième de 12%, c’est-à-dire 1%, soit 100 euros.

Au total, le montant des intérêts s’élèvera, au bout d’un an, à 12 X 100 €, soit à 1.200 €.

Manifestement, cette solution ne revient pas au même selon que l’on se place du point de vue de l’emprunteur ou du prêteur.

En effet, tandis que le premier aurait pu faire fructifier cette somme, le second aurait pu les prêter.

Le taux actuariel tient ainsi compte du facteur temps, à supposer que le prêt des intérêts progressivement versés rapporte des intérêts composés de 1% par mois. L’intérêt produit par le capital d’un euro au bout d’un mois étant de 0,01 euros, ledit capital prend la valeur de 1,01 euros à l’issue de cette période.

Selon la méthode proportionnelle, le taux actuariel assure l’égalité entre, d’une part, les sommes prêtées et, d’autre part, tous les versements dus par l’emprunteur au titre de ce prêt, en capital, intérêts et frais divers.

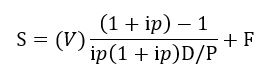
Avec :

• S = Somme prêté
• V = versement périodique
• Ip = intérêt périodique
• P = période
• F = frais divers

Dans un second temps, il convient, pour obtenir le taux effectif global, de multiplier le taux de période par le nombre de période que comporte l’année civile.

L’article R. 314-2 dispose en ce sens que « lorsque les versements sont effectués avec une fréquence autre qu’annuelle, le taux effectif global est obtenu en multipliant le taux de période par le rapport entre la durée de l’année civile et celle de la période unitaire ».

Avec :

• K = constante de calcul relative à la période

S’agissant de l’ouverture d’une ligne de crédit à court terme, l’alinéa 3 de cette disposition prévoit que le TEG qui figure sur la convention de compte, doit être calculé sur la totalité des droits mis à la disposition du client, comme si l’entreprise avait mobilisé l’intégralité de sa ligne de tirage sur la durée théorique de cette possibilité de tirage.

Ainsi, la méthode proportionnelle conduit, au fond, à exprimer le taux effectif global en un taux proportionnel, car en relation, de façon proportionnelle, au taux de période.

II) Le calcul du TAEG : la méthode équivalente

L’article R. 314-3, al. 1^er du Code de la consommation prévoit que le coût des crédits consentis à des consommateurs, qui s’exprime en taux annuel effectif global, se calcule selon la méthode d’équivalence.

À la différence de la méthode proportionnelle, la méthode équivalente n’exige pas, pour calculer le taux effectif global, de déterminer, au préalable, le taux de période : il évalue directement un taux annuel. Cette particularité permet d’obtenir un taux effectif global plus juste.

En effet, s’il est d’usage que les établissements bancaires communiquent sur un taux de crédit annuel, la périodicité de remboursement est, le plus souvent, mensuelle.

La question qui alors se pose est de savoir comment convertir un taux débiteur annuel en un taux débiteur mensuel. Cette conversion s’impose dès lors que l’on exige de l’emprunteur qu’il rembourse, chaque mois, les intérêts correspondant à la rémunération du prêteur.

Lorsque l’on applique la méthode proportionnelle, il suffit, pour déterminer le taux de période, de recourir à une simple division. Lorsque, en revanche, l’on recourt à la méthode équivalente, l’opération est bien moins évidente, car elle repose sur le calcul du taux équivalent.

Des taux d’intérêt se rapportant à des périodes différentes sont dits équivalents si la valeur future d’une même somme à une même date est la même avec chaque taux.

Contrairement à la méthode proportionnelle, la méthode équivalente conduit ainsi à l’obtention d’un taux débiteur annuel qui peut varier selon la périodicité des versements.

Cette méthode met toutefois en œuvre, une formule plus lourde qu’une division : elle repose sur un calcul d’actualisation des flux à compter de la date de déblocage des fonds.

L’article R. 314-3, al. 2 prévoit en ce sens que « le taux annuel effectif global est calculé actuariellement et assure, selon la méthode des intérêts composés, l’égalité entre, d’une part, les sommes prêtées et, d’autre part, tous les versements dus par l’emprunteur au titre de ce prêt pour le remboursement du capital et le paiement du coût total du crédit au sens du 7° de l’article L. 311-1 ces éléments étant, le cas échéant, estimés. »

Concrètement, la détermination du taux effectif global procède de la résolution d’une équation mathématique – énoncée à l’article 2 du décret du 29 juin 2016[1] – qui vise à égaliser le total (actualisé) des sommes prêtées et des échéances dues par l’emprunteur, selon la formule suivante :

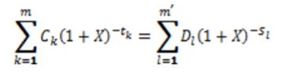
Avec :

• X est le TAEG ;
• m désigne le numéro d’ordre de la dernière utilisation effectuée sur le crédit ;
• k désigne le numéro d’ordre de la dernière utilisation effectuée sur le crédit, donc 1 ≤ k ≤ m ;
• Ck est le montant de la dernière utilisation effectuée sur le crédit numéro k ;
• tk désigne l’intervalle de temps, exprimé en années et fractions d’année, entre la date de la première utilisation effectuée sur le crédit et la date de chacune des utilisations suivantes effectuées, donc t 1 = 0 ;
• m’ est le numéro d’ordre du dernier remboursement ou paiement de frais ;
• l est le numéro d’ordre d’un remboursement ou paiement de frais ;
• Dl est le montant d’un remboursement ou paiement de frais ;
• sl est l’intervalle de temps, exprimé en années et fractions d’années, entre la date de la première utilisation effectuée sur le crédit et la date de chaque remboursement ou paiement de frais.

Cette équation représente l’égalité entre la, ou, les mises à disposition des fonds et tous les remboursements ou dépenses, actualisés à la date du premier déblocage.

Au bilan, il apparaît que c’est désormais la méthode équivalente qui s’impose comme la méthode de calcul de référence du coût du crédit.

Sous l’impulsion du législateur européen, elle est d’application générale, tandis que le recours à la méthode proportionnelle est circonscrit au domaine des seuls crédits consentis aux professionnels et aux personnes morales de droit public

Si, à cet égard, il échoit aux établissements bancaires de bien distinguer selon les deux catégories de crédits envisagées par le Code de la consommation afin de déterminer la méthode applicable au calcul du taux, il leur appartient, en toute hypothèse, de communiquer à l’emprunteur, préalablement à la conclusion du contrat de crédit, le coût de l’opération, exprimé, tantôt en TAEG, tantôt en TEG.

[1] Décret no 2016-884 du 29 juin 2016 relatif à la partie réglementaire du code de la consommation: https://www.legifrance.gouv.fr/jo_pdf.do?id=JORFTEXT000032797752.